Gebruiker:Franciscus/kladblok

Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)

Edward Elgar omstreeks 1925

>> Paul Dukas ( 1865 - 1935 ) >

1. 2 ²/ ₉ + ⁵/ ₉ = 2 ⁷/ ₉

Franciscus 20 jul 2009 13:33 (UTC)

• sin α = BC / AB = ½ AB / AB = 0,5

Voor zijde AC wordt de stelling van Pythagoras toegepast, en wel als volgt:

• AC = √ ( AB ) ² – ( BC ) ² = √ ( AB ) ² – ( ½ AB ) ² = √ ¾ (AB) ² = ½ AB√3

Hieruit volgt dan :

• cos α = AC / AB = ½ AB √ 3 / AB = ½ √ 3 ( = 8,66 )

en :

• tg α = BC / AC = ½ AB / ½ AB√3 = 1/3 . √3 = 0,577

Quotiënt	Φ
1 : 1	1
2 : 1	2
3 : 2	1,5
5 : 3	1,67
8 : 5	1,6
13 : 8	1.62500
89 : 55	1,6181818
610 : 377	1,61537135
4181 : 2584	1,61803405
28657 : 17711	1,61803399
196418 : 121393	1,618033989

Rekenkunde ( 6 )

In Rekenkunde ( 5 ) werden de Breuken behandeld met hun specifieke eigenschappen.
In dit artikel wordt met de nodige voobeelden aandacht besteed aan:

• Samengestelde breuken
• Herleiden van breuken naar decimale getallen
• Herleiden van decimale getallen naar breuken
• Vereenvoudiging van breuken met de Grootste Gemene Deler ( GGD )
• Ontbinden in factoren
• Vereenvoudiging van breuken met het Kleinste Gemene Veelvoud ( KGV )

Samengestelde breuken

Twee samengestelde breuken zijn te vinden in :
Voorbeeld 1

3 / 4 ------ 5 / 8 en : 5 5 / 6 ------ 5 1 / 4

Deze samengestelde breuken kunnen door deling worden herleid tot gewone breuken.
Voorbeeld 2

3 / 4 ------- = 3 / 4 : 5 / 8 = 3 / 4 • 8 / 5 5 / 8 Na vereenvoudiging wordt dit : 3 • 2 / 5 = 6 / 5 = 1 1 / 5

Door de 2 ^e breuk om te keren, wordt de deling een vermenigvuldiging!
Voorbeeld 3

5 5 / 6 -------- = 35 / 6 : 21 / 4 = 35 / 6 • 4 / 21 5 1 / 4 Na vereenvoudiging wordt dit : 5 / 3 • 2 / 3 = 10 / 9 = 1 1 / 9

Herleiden van breuken naar decimale getallen

Sommige breuken kunnen eenvoudig worden herleid naar decimale breuken.
Twee samengestelde breuken zijn te vinden in :
Voorbeeld 4

4 / 5 en: 3 3 / 5

Uitgewerkt geeft dit:

4 / 5 Vermenigvuldig teller en noemer met 2 : 8 / 10 = 0,8

En ook:

3 3 / 5 Vermenigvuldig teller en noemer met 2 : 3 6 / 10 = 3,6

Herleiden van decimale getallen naar breuken

Sommige decimale getallen kunnen eenvoudig worden herleid naar breuken.
Voorbeeld 5

7,5 = 7 5 / 10 = 7 1 / 2

Voorbeeld 6

8,225 = 8 225 / 1000 Teller en noemer delen door 25 : 8 9 / 40

Grootste gemene deler ( GGD )

Voor het vereenvoudigen van grote breuken, wordt gebruik gemaakt van de grootste gemene deler. Hierbij worden zowel de teller als de noemer door het grootst mogelijke getal gedeeld.
Voorbeeld 7

315 / 420 Delen door 5 = 63 / 84 Delen door 3 = 21 / 28 Delen door 7 = 3 / 4 = 0,75 De grootste gemene deler = 5 • 3 • 7 = 105

Ontbinden in factoren

Alvorens met het kleinste gemene veelvoud aan de slag te gaan, is het nodig even een uitstapje te maken naar het ontbinden in factoren.
Bij het ontbinden in factoren wordt een getal ontleed in de kleinst mogelijke factoren, die alleen door zich zelf deelbaar zijn. Dit worden ook wel priemgetallen genoemd.
De priemgetallen tussen 1 en 20 zijn :

• 1
• 2
• 3
• 5
• 7
• 11
• 13
• 17
• 19

Voorbeeld 8

150 = 2 • 75 150 = 2 • 3 • 25 150 = 2 • 3 • 5 • 5 150 = 2 • 3 • 5 2

Ook zeer grote getallen kunnen worden ontbonden in factoren.
Voorbeeld 9

8820 = 2 • 4410 8820 = 2 • 2 • 2205 8820 = 2 2 • 3 • 735 8820 = 2 2 • 3 • 3 • 245 8820 = 2 2 • 3 2 • 5 • 49 8820 = 2 2 • 3 2 • 5 • 7 2

Kleinste gemene veelvoud ( KGV )

Als een aantal breuken met verschillende noemers moet worden opgeteld, dan moeten deze noemers aan elkaar gelijk worden gemaakt.
Voorbeeld 10

1 / 2 + 2 / 3 + 4 / 5 Het KGV = 30, zodat: 15 / 30 + 20 / 30 + 24 / 30 = 59 / 30 = 1 29 / 30

Met deze relatief kleine noemers is het vrij eenvoudig het KGV vast te stellen. Anders wordt het, als de noemers groot worden.
Voorbeeld 11

5 / 8 - 3 / 7 + 31 / 120 De eerste noemer 8 wordt ontbonden in : 2 3 De tweede noemer 7 kan niet verder worden ontbonden De derde noemer 120 wordt ontbonden in : 2 3 • 3 • 5 Het KGV is opgebouwd uit de grootste gevonden elementen : 2 3 • 3 • 5 • 7 = 840 De uitkomst van de breuk wordt nu : 525 / 840 - 315 / 840 + 217 / 840 = 382 / 840 = 191 / 420

Rekenkunde ( 7 )

Het onderwerp Rekenkunde wordt afgesloten met een aantal bijzondere onderwerpen, te weten:

• De kenmerken van deelbaarheid van een getal
• Worteltrekken door ontbinden in factoren
• Procent en promille
• Verhoudingen en evenredigheden

Kenmerken van deelbaarheid

Aan een getal kan meestal na enige inspanning worden gezien of dit deelbaar is door een priemgetal.
Een geheel getal is deelbaar door een ander geheel getal als bij de deling de rest 0 is. Zo is 35 deelbaar door 5, want 35 : 5 = 7 rest 0.
Het getal 38 is niet deelbaar door 7, want 38 : 7 = 5 rest 2.
Om de deelbaarheid van een geheel getal te kunnen achterhalen, bestaan eenvoudige middelen : de zogeheten

• kenmerken van deelbaarheid.

Dit nagaan van de deelbaarheid zal zich uitstrekken tot de deelbaarheid van een getal door 11.

Deelbaarheid door 2

• Een getal is deelbaar door 2, als het laatste cijfer een even cijfer is, namelijk 0, 2, 4, 6 of 8.

Voorbeeld 1

Het getal 123456 is deelbaar door 2 , want 6 is deelbaar door 2

Deelbaarheid door 3

• Een getal is deelbaar door 3, als de som van de cijfers deelbaar is door 3.

Voorbeeld 2

Het getal 12345 is deelbaar door 3 , want 1 + 2 + 3 + 4 + 5 = 15 15 is deelbaar door 3

Deelbaarheid door 4

• Voor getallen bestaande uit twee of meer cijfers is de deelbaarheid door 4 eenvoudig vast te stellen, als het getal van de laatste twee cijfers deelbaar is door 4.

Voorbeeld 3

Het getal 123456 is deelbaar door 4, want 56 is deelbaar door 4

Deelbaarheid door 5

• Een getal is deelbaar door 5, als het laatste cijfer deelbaar is door 5.

Voorbeeld 4

Het getal 12345 is deelbaar door 5, want het laatste cijfer = 5

• Merk op, dat het getal 12345 uit Voorbeeld 2 zowel deelbaar is door 3, als door 5, zodat het getal

12345 deelbaar is door 15

Deelbaarheid door 6

• Een getal is deelbaar door 6, als het getal zowel door 2 als door 3 deelbaar is.
• Merk op, dat het getal 123456 uit Voorbeeld 1, zowel deelbaar is door 2 als door 3, dus door 6.

Deelbaarheid door 7

• Voor getallen >100 is de deelbaarheid door 7, vast te stellen, als het getal, dat wordt verkregen door het laatste cijfer weg te laten en 2 maal af te trekken van het getal gevormd door de overblijvende cijfers.

Voorbeeld 5

Het getal 476 is deelbaar door 7 , want 47 - 2 • 6 = 35 35 is deelbaar door 7

Deelbaarheid door 8

• Voor getallen bestaande uit drie of meer cijfers, is de deelbaarheid door 8 eenvoudig vast te stellen, als het getal van de laatste drie cijfers deelbaar is door 8.

Voorbeeld 6

Het getal 123456 is deelbaar door 8, want 456 is deelbaar door 8

Deelbaarheid door 9

• Een getal is deelbaar door 9 , als de som van de cijfers deelbaar is door 9.

Voorbeeld 7

Het getal 44424 is deelbaar door 9 , want 4 + 4 + 4 + 2 + 4 = 18 18 is deelbaar door 9

• Merk op, dat het getal 44424 uit Voorbeeld 7, zowel deelbaar is door 9 als door 8, dus door 72.

Deelbaarheid door 10

• Een getal is deelbaar door 10, als het laatste getal een 0 is.

Deelbaarheid door 11

• Voor getallen >100 is de deelbaarheid van 11, vast te stellen, als de som van de cijfers op de oneven plaatsen min de de som van de cijfers op de even plaatsen deelbaar is door 11.

Voorbeeld 8

Het getal 1617 is deelbaar door 11 , want 7 - 1 + 6 - 1 = 11

Worteltrekken door ontbinden in factoren

Soms kan het worteltrekken op een eenvoudiger manier worden uitgevoerd, dan is omschreven in Rekenkunde ( .. ).
Het blijkt, dat - door gebruik te maken van het ontbinden in factoren - het oplossen van wortelvormen sneller kan verlopen.
Voorbeeld 9

• √ 63504

63504 = 2 • 31752 63504 = 2 • 2 • 11907 63504 = 2 2 • 2 • 15876 63504 = 2 3 • 2 • 7938 63504 = 2 4 • 2 • 3969 63504 = 2 4 • 3 • 1323 63504 = 2 4 • 3 • 3 • 441 63504 = 2 4 • 3 2 • 3 • 147 63504 = 2 4 • 3 3 • 3 • 49 63504 = 2 4 • 3 4 • 7 • 7 63504 = 2 4 • 3 4 • 7 2

• De vorm √ 63504 is nu teruggebracht tot √ 2 ⁴ • 3 ⁴ • 7 ² , waarvan de uitkomst dus is :

2 ² • 3 ² • 7 = 4 • 9 • 7 = 252

Procent en promille

In economische beschouwingen en in elektrotechnische en andere vakgebieden, wordt vaak met procenten ( = percentages ) van getallen gewerkt. Ook promillages komen hierbij aan de orde.

Procent

De aanduiding procent ( % ) of percent betekent letterlijk : een deel per honderd = ¹ / ₁₀₀ = 0,01.
Voorbeeld 10

75% van 144 = 3 / 4 van 144 = 3 • 144 / 4 = 108

Promille

De aanduiding promille ( ‰ ) betekent letterlijk : een deel per duizend = ¹ / ₁₀₀₀ = 0,001.
In de chemie komen promillages vrij geregeld voor.
Voorbeeld 11

2 2 / 3 ‰ van 900 = 8 / 3 • 900 / 1000 = 2 2 / 5 = 2,4

Verhoudingen en evenredigheden

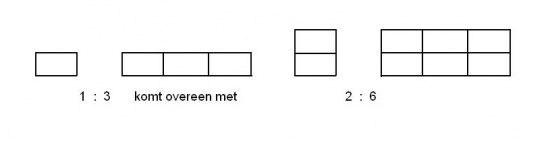
Verhoudingen

In de afbeeldingen wordt duidelijk gemaakt wat bedoeld wordt met verhoudingen.
De verhouding in de 1 ^e afbeelding is gelijk aan de verhouding in de 2 ^e afbeelding.

Evenredigheden

Een evenredigheid geeft de gelijkheid aan van twee verhoudingen.
Voorbeeld 12 :

1 : 3 = 2 : 6

Van deze evenredigheid zijn:

1 en 2 de termen van de eerste reden 3 en 6 de termen van de tweede reden 3 en 2 de middelste termen 1 en 6 de buitenste termen

Eigenschappen

Gelijkblijvende evenredigheid

Als de termen van de eerste reden met eenzelfde getal worden vermenigvuldigd of worden gedeeld, dan verandert dit niets aan de evenredigheid. Hetzelde geldt voor de termen van de tweede reden.

Voorbeeld 13 :

1 : 3 = 2 : 6 wordt na vermenigvuldiging met 5 : 1 • 5 : 3 • 5 = 2 : 6 of na deling door 5 : 1 / 5 : 3 / 5 = 2 : 6

Als bij de 1 ^e term van de eerste reden de 1 ^e term van de tweede reden wordt opgeteld, en 2 ^e term van de eerste reden de 2 e term van de tweede reden wordt opgeteld, dan verandert dit niets aan de evenredigheid.

Voorbeeld 14 :

1 : 3 = 2 : 6 wordt : ( 1 + 2 ) : ( 3 + 6 ) = 2 : 6

Verandering van de evenredigheid

Een verandering van de evenredigheid treedt op, als de termen van de eerste reden worden opgeteld, en ook de termen van de tweede reden.

Voorbeeld 15 :

1 : 3 = 2 : 6 wordt : ( 1 + 3 ) : ( 2 + 6 ) = 1 : 2 = 3 : 6

Vierde evenredige

Als de buitenste termen van een verhouding met elkaar worden vermenigvuldigd en ook de binnenste termen met elkaar worden vermenigvuldigd, dan is het product daarvan gelijk.

Voorbeeld 15 :

3 : 5 = 9 : 15 dit wordt dan : 3 • 15 = 45 en 5 • 9 = 45

Deze eigenschap wordt ook wel de hoofdeigenschap van de evenredigheden genoemd.

Middelevenredige

Bij de middelevenredige zijn de middelste termen aan elkaar gelijk.

Voorbeeld 16 :

3 : 9 = 9 : 27 dit wordt bij toepassing van de 4 e evenredige : 9 • 9 = 81 en 3 • 27 = 81

Als bij een vraagstuk de middelste termen niet bekend zijn, dan kunnen deze eenvoudig worden vastgesteld.

Voorbeeld 17 :

De onbekende middelste termen noemt men : x 6 : x = x : 150 dit wordt : x 2 = 6 • 150 = 900 waardoor : x = √ 900 = 30

Met de invoering van X als vervanging van een getal, wordt een ander gebied betreden, namelijk de Algebra.

De serie artikelen over Rekenkunde wordt om die reden hier afgesloten.

Het vak Algebra wordt vaak toegepast bij technische vraagstukken die ingewikkelde beredeneringen

met zich meebrengen en daardoor vaak tot lange becijferingen met grote getallen leiden.

Dit is de belangrijkste reden waarom bij Algebra naast cijfers ook letters worden gebruikt.

Links

• Rekenkunde ( 1 ) : Optellen en aftrekken
• Rekenkunde ( 2 ) : Vermenigvuldigen, delen en worteltrekken
• Rekenkunde ( 3 ) :
• Rekenkunde ( 4 ) :
• Rekenkunde ( 5 ) :
• Rekenkunde ( 6 ) : Samengestelde breuken, kenmerken van deelbaarheid