Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok: verschil tussen versies
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| Regel 347: | Regel 347: | ||
<tr> | <tr> | ||
<td align="center" bgcolor=#fff7cb> | <td align="center" bgcolor=#fff7cb> | ||
<span style="font-size:125%;"><font color=black>'''<sup> 1</sup>/<sub> 3</sub> + <sup> 2</sup>/<sub> 3</sub> = <sup> = 3</sup>/<sub> | <span style="font-size:125%;"><font color=black>'''<sup> 1</sup>/<sub> 3</sub> + <sup> 2</sup>/<sub> 3</sub> = <sup>3</sup>/<sub> 3</sub> = 1'''</font></span> | ||
</td> | |||
</tr> | |||
</table> | |||
In '''''Voorbeeld 2''''' wordt getoond, dat optellen en aftrekken in één bewerking voorkomen: | |||
<table width="25%" border="1"> | |||
<tr> | |||
<td align="center" bgcolor=#fff7cb> | |||
<span style="font-size:125%;"><font color=black>'''<sup> 3</sup>/<sub> 8</sub> - <sup> 5</sup>/<sub> 8</sub> + <sup>4</sup>/<sub> 8</sub> = <sup>2</sup>/<sub> 8</sub> = <sup>1</sup>/<sub> 4</sub>'''</font></span> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
==Combinaties== | ==Combinaties== | ||
Een ander voorbeeld laat zien, dat ook combinaties van hele getallen met breuken kunnen voorkomen. | Een ander voorbeeld laat zien, dat ook combinaties van ''hele'' getallen met ''breuken'' kunnen voorkomen. | ||
<br/>'''''Voorbeeld | <br/>'''''Voorbeeld 3''''' | ||
<table width=" | <table width="25%" border="1"> | ||
<tr> | <tr> | ||
<td align="center" bgcolor=#fff7cb> | <td align="center" bgcolor=#fff7cb> | ||
:<span style="font-size:125%;"><font color=black>'''3<sup> 2</sup>/<sub> 9</sub> | :<span style="font-size:125%;"><font color=black>'''3 <sup> 2</sup>/<sub> 9</sub> - 4 <sup> 5 </sup>/<sub> 9</sub> + 7 <sup> 8</sup>/<sub> 9</sub> '''</font></span> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Dit gaat als volgt: | Dit gaat als volgt: | ||
<table width=" | <table width="25%" border="1"> | ||
<tr> | <tr> | ||
<td align="left" bgcolor=#fff7cb> | <td align="left" bgcolor=#fff7cb> | ||
<span style="font-size:125%;"><font color=black> | <span style="font-size:125%;"><font color=black> | ||
*''' 3 + | *''' 3 - 4 + 7 = 6''' | ||
*<sup> '''2</sup>/<sub> 9</sub> + <sup> | *<sup> '''2</sup>/<sub> 9</sub> - <sup> 5</sup>/<sub> 9</sub> + <sup> 8</sup>/<sub> 9</sub> = <sup>5</sup>/<sub> 9</sub> ''' <br/> | ||
* ''' | * '''6 + <sup> 5</sup>/<sub> 9</sub> = 6<sup> 5</sup>/<sub> 9 </sub>''' </font></span> | ||
Versie van 3 feb 2010 12:18
Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)


- 2 2/ 9 + 5/ 9 = 2 7/ 9
Franciscus 20 jul 2009 13:33 (UTC)
- sin α = BC / AB = ½ AB / AB = 0,5
- Voor zijde AC wordt de stelling van Pythagoras toegepast, en wel als volgt:
- AC = √ ( AB ) 2 – ( BC ) 2 = √ ( AB ) 2 – ( ½ AB ) 2 = √ ¾ (AB) 2 = ½ AB√3
- Hieruit volgt dan :
- cos α = AC / AB = ½ AB √ 3 / AB = ½ √ 3 ( = 8,66 )
- en :
- tg α = BC / AC = ½ AB / ½ AB√3 = 1/3 . √3 = 0,577
| Quotiënt | Φ |
|---|---|
| 1 : 1 | 1 |
| 2 : 1 | 2 |
| 3 : 2 | 1,5 |
| 5 : 3 | 1,67 |
| 8 : 5 | 1,6 |
| 13 : 8 | 1.62500 |
| 89 : 55 | 1,6181818 |
| 610 : 377 | 1,61537135 |
| 4181 : 2584 | 1,61803405 |
| 28657 : 17711 | 1,61803399 |
| 196418 : 121393 | 1,618033989 |
Rekenkunde ( 4 )
In Rekenkunde ( 1 ), ( 2 ) en ( 3 ) zijn de diverse basisbegrippen van de Rekenkunde behandeld.
Bij de diverse bewerkingen die daar aan de orde kwamen, moet - als ze in combinatie met elkaar optreden - altijd een bepaalde volgorde worden aangehouden. Wordt dit niet gedaan, dan ontstaan fouten in de bewerkingen.
Verder wordt in dit artikel aandacht besteed aan Decimale getallen en aan Breuken. Ook de bijbehorende bewerkingen -
Volgorde van de bewerkingen
De volgorde van de diverse bewerkingen - zoals in Rekenkunde ( 1 ), ( 2 ) en ( 3 ) behandeld - moet altijd als volgt verlopen:
|
- Soms wordt om deze volgorde te onthouden, het volgende 'ezelsbruggetje' toegepast:
- (M) ijnheer (V) an (D) alen (W) acht (O) p (A) ntwoord
- Voorbeeld 1
|
12 3 • 3 : 9 - √ 36 + 5 - 3 =
|
Hulpmiddelen
Als van de normale volgorde moet worden afgeweken, dan worden soms hulpmiddelen gebruikt, en wel:
|
- Bij gebruik van deze hulpmiddelen wordt eerst uitegerekend wat binnen de haakjes staat. Daarna wordt vastgesteld, wat binnen de accoladen staat, en als laatste wordt nagegaan wat binnen de rechte haakjes staat.
- Nadat de berekeningen zijn gemaakt, worden achtereenvolgens de haakjes, de accoladen en de rechte haakjes weggelaten.
- Als de hulpmiddelen zijn verdwenen, wordt de berekening in de normale volgorde voortgezet.
- Voorbeeld 2
|
[ { ( 28 - 16 ) • 3 - ( 12 + 4 ) : 4 } • √ 25 - 10 ]:{( 4 + 3 )• 2 3 - 6 } =
|
Decimale getallen
Decimale getallen zijn getallen waar een komma in voorkomt.
- Voorbeeld 3
|
Optellen en aftrekken van decimale getallen
Als deze drie getallen met elkaar moeten worden opgeteld, dan wordt gehandeld zoals in Rekenkunde ( 1 ) werd uitgelegd, door de getallen met de komma's onder elkaar te zetten, en verder te handelen als daar omschreven, aldus:
- Voorbeeld 4
|
Het aftrekken van decimale getallen gaat als volgt:
- Voorbeeld 5
|
In de uitkomst mag de 0 achter de 3 worden weggelaten, zodat dus 85,32 - 36,02 = 49,3
Vermenigvuldigen en delen van decimale getallen
Als decimale getallen met elkaar moeten worden vermenigvuldigd, dan wordt gehandeld zoals in Rekenkunde ( 2 ) werd uitgelegd, door de getallen met de komma's onder elkaar te zetten, en verder te handelen als daar omschreven.
- Voorbeeld 6
- 67,123 • 4,25
|
Bij het vermenigvuldigen worden de te vermenigvuldigen getallen onder elkaar geplaatst en verder bewerkt, waarbij het kleinste getal onder wordt gezet. Als de uitkomst van een bewerking 10 is of groter is dan 10, dan moet het linker deel hiervan worden onthouden en bij de volgende bewerking worden toegevoegd.
Delen
Bij decimale getallen gebeurt het delen op dezelfde manier als in Rekenkunde ( 1 ) werd behandeld. Alleen het plaatsen van de komma vraagt extra aandacht.
- Voorbeeld 7
|
12,75 : 0,5 = 25,5 |
Niet alle delingen zijn zó eenvoudig op te lossen, zoals uit het volgende voorbeeld blijkt:
- Voorbeeld 8
|
55,53819 : 7,093 |
Om hier eenvoudig mee te kunnen rekenen, wordt in beide getallen de komma drie plaatsen naar rechts verplaatst, waardoor de deling overzichterlijker wordt.Dit wordt aldus genoteerd:
|
Eerst wordt nagegaan, welk veelvoud van 7093 het dichts bij 55538 komt. Dit blijkt 49651 = 7 • 7093 te zijn. Dit getal wordt afgetrokken, zodat de rest 5887 is. Voordat de 1 naar onder wordt gebracht, moet een komma achter de 7 worden geplaatst.
Als de 1 is aangehaald, blijkt 8 • 7093 = 56744 dicht bij 58871 te liggen, waardoor een rest van 21279 overblijft. Het blijkt, dat 3 • 7093 = 21279, zodat de rest = 0. Het blijkt dus, dat:
|
55,53819 : 7,093 = 7,83 |
Niet opgaande deling
Onder decimale getallen vallen ook bewerkingen waarbij na een niet opgaande deling verder wordt berekend in één of meer decialen.
- Voorbeeld 9
|
18432 : 180 |
Dit gaat als volgt:
|
18432 : 180 = 11,4
De deling verloopt aanvankelijk op de gebruikelijke manier. Bij het getal 432 aangekomen, blijkt de deling nog niet uitgekomen te zijn. Hier wordt dan verder gegaan, door er een 0 bij te halen en verder te delen.
Machtsverheffen
Machtsverheffen met decimale getallen gaat in principe op dezelfde manier als gewone getallen. Het enige verschil is, dat er rekening met de komma's gehouden moet worden.
- Voorbeeld 10
|
0,8135 2 = 0,8135 • 0,8135 = 0,66178225 |
Het blijkt, dat er 4 cijfers achter het getal 0,8135 staan, zodat er dus in de uitkomst 2 • 4 = 8 cijfers achter de komma moeten verschijnen, zoals de berekening ook aangeeft.
Worteltrekken
Ook worteltrekken uit decimale getallen gaat in principe op gelijke wijze als bij gewone getallen, mits rekening wordt gehouden met de komma's.
- Voorbeeld 11
|
√ 155,0025 |
Om de vorm √ 155,0025 op te lossen, wordt als volgt te werk gegaan:
- Verdeel het getal vanaf de rechterkant in groepen van 2 cijfers, dus: 1 | 55,| 00 | 25
- Zoek het grootste getal, dat in het kwadraat zó dicht mogelijk bij het linker getal ligt,dus: 1 • 1 = 1. De 1 wordt als eerste getal van de uitkomst genoteerd.
- De verschil tussen 1 en 1 is 0
- Tel hierna de cijfers van de eerste bewerking op, dus: 1 + 1 = 2
- Zoek bij dit getal het cijfer in dit geval ook een 2 - dat achter de al aanwezige 2 wordt geplaatst en vervolgens wordt vermenigvuldigd met 2 = 44, zodat deze uitkomst zó dicht mogelijk bij het getal 55 ligt
- Het gevonden cijfer - de 2 dus - wordt als tweede getal van de uitkomst genoteerd
- Alvorens verder te gaan wordt nu eerst de komma geplaatst
- Bij de volgende stap wordt het cijfer 4 gevonden en bij de laatste stap wordt dit het cijfer 5
De uitkomst van de berekening blijkt te zijn: √ 155,0025 = 12,45
|
Een nieuw ezelsbruggetje is:
- Het Mooie Witte Veulentje Draaft Op en Af ( Haakjes, Machtsverheffen, Worteltrekken, Vermenigvuldigen, Delen, ).
Dit laatste ezelsbruggetje schenkt aandacht aan de haakjes die bij gecompliceerde bewerkingen soms nodig zijn. Bij de behandeling van de breuken en tiendelige breuken zullen ook wortels getrokken worden uit getallen die geen kwadraat van een geheel getal vormen, bijvoorbeeld √ 51.
Rekenkunde ( 5 )
In Rekenkunde ( 4 ) zijn Decimale getallen behandeld met hun specifieke eigenschappen. Naast de decimale getallen worden echter in de dagelijkse praktijk ook 'gewone' breuken gebruikt.
In dit artikel wordt met de nodige voobeelden aandacht besteed aan Breuken, met de bijbehorende bewerkingen.
Verder........................
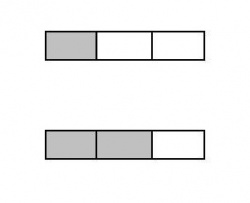
Breuken
Het getal 1/ 3 wordt een breuk genoemd. Dit wordt aanschouwelijk gemaakt door de afbeelding. Het grijs gemaakte gedeelte is 1/ 3 deel van de rechthoek, en bij de tweede afbeelding maken de grijze vlakken 2/ 3 deel van de rechthoek uit.
Optellen en aftrekken
Voorbeeld 1
Als bij 1/ 3
het getal 2/ 3
wordt opgeteld, dan is de afgebeelde rechthoek compleet.
Aldus :
|
1/ 3 + 2/ 3 = 3/ 3 = 1 |
In Voorbeeld 2 wordt getoond, dat optellen en aftrekken in één bewerking voorkomen:
|
3/ 8 - 5/ 8 + 4/ 8 = 2/ 8 = 1/ 4 |
Combinaties
Een ander voorbeeld laat zien, dat ook combinaties van hele getallen met breuken kunnen voorkomen.
Voorbeeld 3
|
Dit gaat als volgt:
|
|
