Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok
Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)


- 2 2/ 9 + 5/ 9 = 2 7/ 9
Franciscus 20 jul 2009 13:33 (UTC)
- sin α = BC / AB = ½ AB / AB = 0,5
- Voor zijde AC wordt de stelling van Pythagoras toegepast, en wel als volgt:
- AC = √ ( AB ) 2 – ( BC ) 2 = √ ( AB ) 2 – ( ½ AB ) 2 = √ ¾ (AB) 2 = ½ AB√3
- Hieruit volgt dan :
- cos α = AC / AB = ½ AB √ 3 / AB = ½ √ 3 ( = 8,66 )
- en :
- tg α = BC / AC = ½ AB / ½ AB√3 = 1/3 . √3 = 0,577
| Quotiënt | Φ |
|---|---|
| 1 : 1 | 1 |
| 2 : 1 | 2 |
| 3 : 2 | 1,5 |
| 5 : 3 | 1,67 |
| 8 : 5 | 1,6 |
| 13 : 8 | 1.62500 |
| 89 : 55 | 1,6181818 |
| 610 : 377 | 1,61537135 |
| 4181 : 2584 | 1,61803405 |
| 28657 : 17711 | 1,61803399 |
| 196418 : 121393 | 1,618033989 |
Rekenkunde ( 5 )
In Rekenkunde ( 4 ) zijn Decimale getallen behandeld met hun specifieke eigenschappen. Naast de decimale getallen worden echter in de dagelijkse praktijk ook 'gewone' breuken gebruikt.
In dit artikel wordt met de nodige voobeelden aandacht besteed aan Breuken, met de bijbehorende bewerkingen.
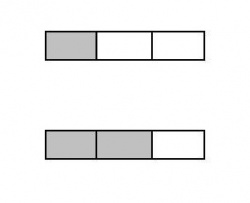
Breuken
Het getal 1/ 3 wordt een breuk genoemd. Dit wordt aanschouwelijk gemaakt door de afbeelding. Het grijs gemaakte gedeelte is 1/ 3 deel van de rechthoek, en bij de tweede afbeelding maken de grijze vlakken 2/ 3 deel van de rechthoek uit.
Optellen en aftrekken
Voorbeeld 1
Als bij 1/ 3
het getal 2/ 3
wordt opgeteld, dan is de afgebeelde rechthoek compleet.
Aldus:
|
|
In Voorbeeld 2 wordt getoond, dat optellen en aftrekken van breuken in één bewerking kunnen voorkomen:
|
|
Combinaties
Een ander voorbeeld laat zien, dat ook combinaties van hele getallen met breuken kunnen voorkomen.
Voorbeeld 3
|
|
Dit gaat als volgt:
|
|
Vermenigvuldigen en delen van breuken
Voorbeeld 4
|
|
De werkwijze is hier als volgt:
- De bovenste getallen met elkaar vermenigvuldigen ( teller • teller )
- De onderste getallen met elkaar vermenigvuldigen ( noemer • noemer )
- Nagaan of vereenvoudiging van de uitkomst mogelijk is
Een ander voorbeeld laat zien, dat ook combinaties van hele getallen met breuken kunnen voorkomen.
Voorbeeld 5
|
|
Om dit op te lossen, wordt als volgt te werk gegaan:
|
|
Door deze bewerking wordt dus:
|
|
- De gevonden vormen opzetten
- Noemers kruislings verwisselen ( uitkomst blijft gelijk )
- Nagaan of verwisselde tellers en noemers door elkaar te delen zijn
- Uitkomsten met elkaar vermenigvuldigen
|
|
Een onverwacht resultaat!
Bij het delen van breuken, kan soms de 2 e breuk worden omgedraaid en daarna met de 1 e breuk worden vermenigvuldigd.
Voorbeeld 6
|
|
Ook bij de combinatie van hele getallen met breuken kan soms de 2 e breuk worden omgedraaid en daarna met de 1 e breuk worden vermenigvuldigd.
Voorbeeld 7
|
|
De teller 35 = 5 • 7 en de noemer 14 = 2 • 7, zodat de vorm kan worden vereenvoudigd tot:
|
|
Machtsverheffen en worteltrekken van breuken
Voorbeeld 8
|
|
betekent:
|
|
Bij combinatie met een heel getal, wordt een machtsverheffing zó genoteerd :
Voorbeeld 9
|
|
Dit wordt dan:
|
|
Bij wortelvormen is de schrijfwijze :
Voorbeeld 10
|
|
wat inhoudt:
|
|
Voor samengestelde getallen geldt:
Voorbeeld 11
|
|
Wat uitgewerkt oplevert:
|
|
Deze vorm kan worden omgezet naar :
|
|
De vorm :
|
|
kan eventueel nog verder worden uitgewerkt.
Rekenkunde ( 6 )
In Rekenkunde ( 5 ) werden de Breuken behandeld met hun specifieke eigenschappen.
In dit artikel wordt met de nodige voobeelden aandacht besteed aan:
- Samengestelde breuken
- Herleiden van breuken naar decimale getallen
- Herleiden van decimale getallen naar breuken
- Vereenvoudiging van breuken met de Grootste Gemene Deler ( GGD )
- Vereenvoudiging van breuken met het Kleinste Gemene Veelvoud ( KGV )
- Ontbinden in factoren
Samengestelde breuken
Twee samengestelde breuken zijn te vinden in :
Voorbeeld 1
|
|
Deze samengestelde breuken kunnen door deling worden herleid tot gewone breuken.
Voorbeeld 2
|
|
Voorbeeld 3
|
|
Herleiden van breuken naar decimale getallen
Sommige breuken kunnen eenvoudig worden herleid naar decimale breuken.
Twee samengestelde breuken zijn te vinden in :
Voorbeeld 4
|
3 3 / 5 |
Uitgewerkt geeft dit:
|
|
En ook:
|
|
Herleiden van decimale getallen naar breuken
Sommige decimale getallen kunnen eenvoudig worden herleid naar breuken.
Voorbeeld 5
|
|
Voorbeeld 6
|
|
Grootste gemene deler ( GGD )
Voor het vereenvoudigen van grote breuken, wordt gebruik gemaakt van de grootste gemene deler.
Hierbij worden zowel de teller als de noemer door het grootst mogelijke getal gedeeld.
Voorbeeld 8
|
De grootste gemene deler = 5 • 3 • 7 = 105
|
Ontbinden in factoren
Alvorens met het kleinste gemene veelvoud aan de slag te gaan, is het nodig even een uitstapje te maken naar het ontbinden in factoren.
Bij het ontbinden in factoren wordt een getal ontleed in de kleinst mogelijke factoren, die zelf niet meer deelbaar zijn. Dit worden ook wel priemgetallen genoemd.
De priemgetallen tussen 1 en 10 zijn :
- 2
- 3
- 5
- 7
Voorbeeld 9
|
|
Ook zeer grote getallen kunnen worden ontbonden in factoren.
Voorbeeld 10
|
|
Kleinste gemene veelvoud ( KGV )
Als een aantal breuken met verschillende noemers moet worden opgeteld, dan moeten deze noemers aan elkaar gelijk worden gemaakt.
Voorbeeld 11
|
|
Met deze relatief kleine noemers is het vrij eenvoudig het KGV vast te stellen. Anders wordt het, als de noemers groot worden.
Voorbeeld 12
|
|
