Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Logaritmen en exponentiële functies
Machtsverheffen
In Rekenkunde ( 3 ) wordt het onderwerp Machtsverheffen behandeld.
Hierbij wordt het volgende gesteld:
- Bij het machtsverheffen wordt een getal één, twee of meer keren met zichzelf vermenigvuldigd, waarbij de volgende schrijfwijze wordt gehanteerd:
|
10 1 = 1 • 10 = 10
|
Voorbeeld 1
|
Als het getal 5 een drietal keren met zichzelf wordt vermenigvuldigd, dus:
|
- Als machten moeten worden vermenigvuldigd met andere machten of worden gedeeld door andere machten die hetzelfde grondtal hebben, dan moeten de exponenten van die machten bij elkaar worden opgeteld of worden afgetrokken
|
10 1 • 10 1 kan worden geschreven als : 10 1+1 = 102 = 10 • 10 = 100
|
Exponenten
Het ligt zeer voor de hand te veronderstellen, dat tussen 10 0 en 10 1 of bijvoorbeeld tussen 10 1 en 10 2 ook machten van 10 liggen die een ander getal dan 1, 10 of 100 zouden kunnen opleveren. Dit blijkt inderdaad het geval te zijn.
In Rekenkunde ( 3 ) wordt het onderwerp Worteltrekken behandeld. De ( vierkants )wortel uit bijvoorbeeld 10 wordt aldus genoteerd:
- √ 10 = 3,1622
|
Een andere schrijfwijze voor de wortel uit 10 is 10 1/2 = 10 0,5 wat hetzelfde oplevert, namelijk 3,1622
|
Om elk getal in een exponent uit te kunnen drukken, zijn voor alle getallen tussen 1 en 99 tabellen opgesteld, die deze notering mogelijk maken.
Men noemt hierbij het getal 10 het grondtal, hoewel hiervoor ook een ander getal zou kunnen worden gekozen. De exponent van de macht wordt hier mantisse genoemd.
Voor getallen < 10 wordt een 0 vóór de mantisse geplaatst. Voor getallen > 10 komt vóór de mantisse een 1 te staan, en bij getallen tussen 100 ( = 10 2 ) en 999 plaatst men een 2 vóór de mantisse. Men noemt deze getallen de wijzer van een logaritme. Op die manier is het mogelijk de logaritme van elk denkbaar getal met een wijzer en een exponent vast te leggen.
Tabel van mantissen
| Getal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 |
- ∞ |
0000 | 3010 | 4771 | 6021 | 6090 |
7782 |
8451 | 9031 | 9542 | |
| 1 | 0000 | 0414 |
0792 |
1139 | 1461 | 1761 | 2041 | 2304 | 2553 | 2788 | |
| 2 | 3010 | 3222 | 3424 | 3617 | 3802 | 3979 | 4150 | 4314 | 4472 | 4624 | |
| 3 | 4771 | 4914 | 5051 | 5185 | 5315 | 5441 | 5563 | 5682 | 5798 | 5911 | |
| 4 | 6021 | 6128 | 6232 | 6335 | 6435 | 6532 | 6628 | 6721 | 6812 | 6902 | |
| 5 | 6990 | 7076 | 7160 | 7243 | 7324 | 7404 | 7482 | 7559 | 7634 | 7709 | |
| enz → t/m 99 |
Voorbeeld 2
|
De mantisse van het getal 6 = 0,7782 → 10
0,7782
= 6
|
Tegenwoordig wordt er niet meer zo uitgebreid gebruik gemaakt van tabellen maar meer van ( wetenschappelijke ) calculators. Ondanks het gemak dat we al lange tijd van deze hulpmiddelen hebben, blijkt het – zeker voor wat de wat ingewikkelde problemen - nog steeds noodzakelijk inzicht te hebben in de basiskennis van de logaritmen, aangezien zonder deze kennis niet wordt begrepen hoe logaritmen werken.
Definitie
Het blijkt dat - met wat hiervoor werd uiteengezet - een definitie is te geven van wat een logaritme van een getal is.
|
Een logaritme van een getal y is de exponent van de macht x waartoe het grondtal moet worden gebracht om het getal y te krijgen. |
Als grondtal wordt – zoals boven werd uitgevoerd - als regel het getal 10 genomen. Hieruit volgt dan:
- y = 10 x
waarbij x de exponent ( mantisse ) is. Deze vorm kan ook op een andere manier worden geschreven, namelijk:
- x = 10 log y
waarbij log de afkorting van de logaritme van het getal y voortelt.
Voorbeeld 3
|
De logaritme van het getal 8, is te schrijven als: 8 = 10 x , en x = 10 log 8
|
Voor de goede orde zou eigenlijk vóór de logaritme steeds de exponent 10 moeten worden genoteerd,
dus 10 log a. In de praktijk laat men voor het gemak meestal de aanduiding 10 vóór de logaritme weg.
Briggse en natuurlijke logaritmen
De tot nu toe gehanteerde logaritmen - met als grondtal 10 - worden ook wel Briggse logaritmen genoemd, naar de wiskundige Henry Briggs. Naast deze logaritmen bestaat ook de natuurlijke of Neperse logaritme met als grondtal e, naar de wiskundige John Napier ( Neper ), waarbij e = 2,7182818.......
De notatie voor de Briggse logaritmen is - zoals al uiteengezet - als volgt:
- 10 log x = log x
De notatie voor de natuurlijke logaritme is als volgt:
- e log x = ln x
Om Briggse logaritmen naar de natuurlijke logaritmen te kunnen omrekenen, geldt:
- log x = 0,4343... ln x
en omgekeerd:
- ln x = 2,3026.... log x
Formules
Algemeen gelden de volgende formules:
- log a • b = log a + log b
- log a : b = log a - log b
- log n√ a = 1/n log a
- log a n = n log a
Voorbeeld 3
|
In de vorm: log a • b = log a + log b, wordt voor a en b ingevuld: log 3 • 4 = log 3 + log 4
|
Voorbeeld 4
|
In de vorm: log a : b = log a - log b, wordt voor a en b ingevuld: log 8 : 4 = log 8 - log 4
|
Voorbeeld 5
|
In de vorm: log n√ a = 1/n log a wordt voor a en n ingevuld: log √ 9 = 1/2 log 9 *)
|
*) Voor n√ a wordt bij een 2emachtswortel meestal gewoon √ a geschreven, dus met weglating van de 2 boven het wortelteken.
Voorbeeld 6
- Nagegaan wordt in hoeveel jaar een kapitaal x, uitgezet tegen 5%, zal zijn verdubbeld
|
Na het eerste jaar is het kapitaal gegroeid tot 1,05 x. In het tweede jaar wordt dit dus ( 1,05 • 1,05 ) x
|
In onderstaande grafiek wordt nog duidelijker hoe deze kapitaalstijging in de tijd verloopt. De y-as van de grafiek heeft een logaritmische schaal, waardoor de stijgende lijn van de grafiek een rechte lijn wordt. Goed te zien is, dat na iets meer dan 14 jaar het uitgezette kapitaal is verdubbeld.

Exponentiële functies
Met Voorbeeld 6 over de kapitaalvermeerdering werd met de vorm 1,05 n x al een overstap gemaakt naar de exponentiéle functies.
Bij het machtsverheffen is het duidelijk geworden, dat getallen genoteerd kunnen worden met een exponent, zoals
4 3 = 4 • 4 • 4 = 64.
Op dezelfde manier kan een serie getallen worden uitgedrukt in exponenten.
- Voorbeeld 7
De volgende eenvoudige serie getallen begint met 1 en wordt vervolgens vermenigvuldigd met 2, aldus:
- 1 • 2 = 2
- 2 • 2 = 2 2 = 4
- 2 • 4 = 2 3 = 8
- dus verder als: 2 n
|
1 888 2 888 4 888 8 888 16 888 32 888 64 888 128 888 256 888 512 888 ........ |
Zo’n serie kan ook worden opgezet voor het getal 3, dus verder als: 3 n
aldus:
|
1 888 3 888 9 888 27 888 81 888 243 888 729 888 2187 888 6561 888 ........ |
Deze series – met de notatie 2 n en 3 n - kunnen worden opgezet met verschillende exponenten, en gelden ook voor alle andere denkbare getallen.
Zo’n reeks wordt een exponentiële functie genoemd.
Schaakbord
Het volgende vraagstuk vormt een mooi sluitstuk van het onderwerp Logaritmen en exponentiële functies.
Op het afgebeelde schaakbord wordt op het 1 e veld 1a een eurocent neergelegd en op het veld 1b 2 eurocenten, waarna steeds na elk veld een verdubbeling plaatsvindt.
Dit houdt in, dat op veld 1f al 1 + 2 + 4 + 8 + 16 + 32 = 63 eurocenten op het bord liggen.
De vraag is nu, hoeveel eurocenten er op het bord komen te liggen als de reeks wordt voortgezet.
Dit wordt een nogal bewerkelijke som, zodat we overgaan op een wat listiger manier,
door namelijk vast te stellen, dat:
|
x = 2 n - 1 , waarbij n het aantal velden betekent en x de som van alle aanwezige eurocenten.
|
- Het is duidelijk, dat:
|
De eurocent die er officieel moet worden afgetrokken op den duur geen rol speelt en dus verder wordt weggelaten uit de berekening. Het bedrag zich zeer snel vermeerdert, doordat er steeds een verdubbeling plaatsvindt en de som van de voorgaande bedragen er steeds bijkomen. |
- Als wordt berekend, hoeveel eurocenten er aanwezig zijn als het middelste veld
- - dus veld 4hofwel het 32 e veld, - wordt bereikt, dan wordt dit:
|
x = 2 32 = 4294967296 eurocent = 42,95 miljoen euro |
- Dit resultaat kan ook via logaritmen worden verkregen.
- Aldus:
|
x = 2 32 , dus log x = 32 log 2 = 32 • 0,301029996 = 9,632959862.
|
Als veld 8h, ofwel het 64 e veld wordt bereikt, dan komen we op een bedrag uit, dat gigantisch groot is; een bedrag, dat vermoedelijk heel wat meer dan de gezamenlijke Europese begroting omvat, namelijk 2 64 = 18,45 • 10 16 euro =
- 18,45 • 10 7 miljard euro!
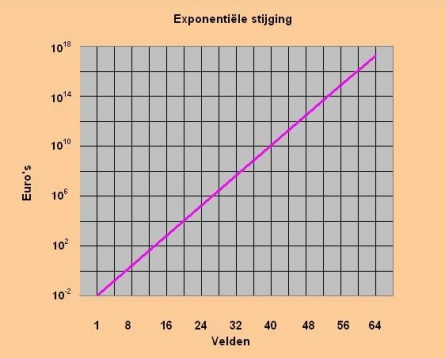
In de grafiek met logaritmische schaal wordt nog sterker be-
nadrukt, hoe gigantisch de stijging van veld 1 ( = 1a )
naar veld 64 = ( 8h ) is.
