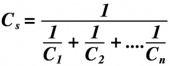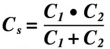Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok
Zoals uit de grafiek blijkt, is de condensatorspanning na 5 • τ gestegen tot ca 100 % van de aangelegde spanning.
Condensator
Een condensator is een passief elektrisch component, dat in veel elektronische schakelingen wordt gebruikt, en een elektrische lading kan opslaan.
De meest eenvoudige condensator bestaat uit een tweetal geleidende platen, die op een geringe afstand van elkaar zijn gescheiden, met daartussen een isolerend materiaal (diëlektricum). De isolerende tussenstof tussen de platen van een condensator kan lucht of polystyreen zijn, papier of een ander isolatiemateriaal.
Een condensator heeft de eigenschap wisselspanning door te laten en gelijkspanning te blokkeren.
Basisformules
Het vermogen van een condensator om een elektrische lading op te slaan wordt de capaciteit genoemd en wordt uitgedrukt in de eenheid farad (symbool F). Als standaardefinitie hiervoor geldt:
- Een condensator die een lading van 1 coulomb bevat terwijl er een spanning van 1 volt tussen de platen staat, heeft een capaciteit van 1 farad.
De spanning over een condensator is rechtevenredig met de lading op de condensator. Het verband tussen de spanning U in volt en de lading Q in coulomb wordt gegeven door:
- Q = C • U
hierin is:
- C de capaciteit in farad (F)
- U de spanning in volt (V)
- In de praktijk wordt (bijna) uitsluitend met microfarad = μF (10 -6F) en met picofarad = pF (10 -12F) gewerkt. Ook wordt wel de term nanofarad = nF (10 -9F) gebruikt.
Capaciteit
De capaciteit C wordt bepaald door:
- Het oppervlak A van de geleiders in m2
- De afstand d tussen de geleiders in m
- De diëlektrische constante ε tussen de geleiders in F/m
Het verband tussen deze grootheden ligt besloten in:
- C = ε . A d
RC-tijd
Als een condensator op een gelijkspanningsbron met een spanning U wordt aangesloten, dan zal de condensator binnen een bepaalde tijd een lading Q aannemen. De snelheid waarmee de condensator wordt geladen, hangt af van de grootte van de weerstand R en de capaciteit van de condensator C.
Het verband tussen R en C wordt uitgedrukt in de tijdconstante τ van de schakeling, waarbij:
- τ = R • C (sec)
Het opladen gebeurt volgens een e-kromme.
- Het getal e – meestal de constante e genoemd – is het grondtal van de natuurlijke logaritme 2,7182818.....
Zoals uit de grafiek blijkt, is de condensatorspanning U na 5τ gestegen tot ongeveer 100 % van de aangelegde spanning U.
- In formulevorm:U = Umax ( 1 - e t / τ )
Ook het ontladen van de condensator gebeurt volgens een e-kromme, maar dan in omgekeerde zin.
- In formulevorm:U = Umax • e t / τ )
- Terwijl de spanning over de condensator toeneemt, neemt de spanning over de weerstand R en de stroom I door de hele schakeling exponentieel af.
Rekenvoorbeeld
De laadtijd berekenen, als R = 20 kΩ en C = 32 μF.
Wisselspanning
Bij een aangelegde wisselspanning wordt de condensator afwisselend geladen, ontladen en tegengesteld geladen, waardoor ( schijnbaar ) stroom wordt doorgelaten. De stroom door de condensator hangt direct samen met de hoeksnelheid ω = 2πf en de capaciteit C van de condensator.
- Op de afbeelding is één periode van een sinusoïde weergegeven, uitgedrukt in de hoeksnelheid ω met als eenheid: radialen/seconde(rad/sec).
Hoe hoger de frequentie, hoe groter de stroom, en ook: hoe groter de capaciteit hoe groter de stroom.
- U = I • Zc = I 1 ωC = waarbij Zc = 1 ωC
Hieruit is de stroom I af te leiden:
- I = U • ωC
Parallelschakelen van condensatoren
Door condensatoren parallel te plaatsen, wordt in feite het oppervlak van de platen vergroot, en neemt de capaciteit toe. Om die reden geldt dan ook, dat de capaciteiten van de condensatoren bij elkaar worden opgeteld, om tot de vervangingscapaciteit Cp te komen.
- Cp = C1 + C2 + …… Cn
De spanning U is voor alle condensatoren gelijk.
Serieschakelen van condensatoren
Door condensatoren in serie te schakelen, wordt de stroom I door elke condensator gelijk, maar vormen de spanningen over de afzonderlijke condensatoren samen de aangelegde spanning U.
Voor de vervangingscapaciteit Cs, geldt het volgende:
Bij twee condensatoren parallel, wordt de formule teruggebracht tot:
Toepassingen
Condensatoren vinden in de elektrotechniek en in de elektronica zeer veel toepassingen. Het gaat te ver om al deze toepassingen hier te noemen, maar de voornaamste hiervan mogen niet ontbreken.
- Tijdelijke opslag van energie: Condensatoren worden gebruikt om veranderingen in elektrische lading te overbruggen en af te vlakken, zoals in gelijkrichters
- Blokkeren van gelijkspanning in filters. Een filter kan worden gebruikt om een ongewenst frequentiegebied uit een signaal te verwijderen
- Het afleiden of blokkeren van hoogfrequente signalen
- Bij TL-verlichting zorgt de condensator in de starter ervoor, dat de optredende hogere harmonischen worden kortgesloten, en dat de onderbreking van de stroom vonkvrij gebeurt
- Compensatie van de faseverschuiving in netten en installaties
Aangezien deze faseverschuiving tot grotere belastingen van het net zorgen, worden aan de grootte daarvan eisen gesteld en moet worden gezorgd, dat een gestelde grens niet wordt overschreden. Dit gebeurt door cosφ - compensatie.
Bij een zuiver ohmse belasting – gevormd door verwarmingsweerstanden of gloeilampen - bereiken de ( sinusvormige ) stroom I en de spanning U beide tegelijkertijd het minimum en het maximum. Door de aanwezigheid van een inductief net zijn de stroom I en de spanning U niet meer in fase met elkaar.
Dat houdt in, dat deze niet gelijktijdig hun maximum of hun minimum bereiken, maar ten opzichte van elkaar verschoven zijn over de hoek φ -> de faseverschuiving.
||i=1 |}
Ψ (x⃗,t)
De stad Montfort-L'Amaury in eerbetoon aan Maurice Ravel die in dit huis van 1921 tot 1937 woonde Ravel se fixa à Montfort-l'Amaury en 1921. Sa maison, le Belvédère, conservée en l'état selon la volonté de son frère, abrite un musée depuis 1971 et fait l’objet d’une inscription auprès des monuments historiques depuis 199459. Français : Maison dite du Belvédère de Maurice Ravel à Montfort-l'Amaury (Yvelines, France) Date 20 November 2006 Source Cliché personnel, own work Author ℍenry Salomé (Jaser !) 08:17, 21 November 2006 (UTC) Object location 48° 46′ 34.28″ N, 1° 48′ 19.4″ E Kartographer map based on OpenStreetMap. View this and other nearby images on: OpenStreetMap - Google Earth info Licensing[edit] The copyright holder of this work, hereby publish it under the following licenses: GNU head Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.
- OPVS FUNDATUM VATICANVM
- Josephvs Ratzinger - Benedictvs XVI
- - Cooperatores Veritatis -
- OPUS FUNDUM VATICANUM
- Josephus Ratzinger - Benedictus XVI
- - Cooperatores Veritatis -
|
|
span>
- Ook in de bioscoop werden antifascistische acties uitgevoerd
|}
Enkele breuken hebben een eigen naam:
- √12
≈12 1 1 = 1
- 2 0 12 = 1
- 2 1 12 = 1,059463094
- 2 2 12 = 1,122462048
x 4
√ L C
|
|
|
|
|
|
|
|
| Op een gegeven moment stelt hij vast,
dat het een verloren zaak is. |
|---|
|
|
- Het schrijven van de Magister Ludi aan de Pedagogische Dienst
|}
|
|
|
|
{{Overline| (12)}}om ergens een lijntje boven te trekken{{Overline|24}}
12
24
12
--
24
Breuken
Bestand:Rmath.png

a b⁄c: a b/c (geheel getal, teller en noemer)
a⁄b: a/b (teller en noemer)
1⁄a: 1/a (alleen noemer)
12
--
24
{{Overline|a}}
12
24
a
{{Overline|24}}
12
24
Sjabloon:I =vbreuk
In deze theoretische verhandeling, wordt de vergelijking:
S = A L geïntroduceerd.
Hierbij is:
- S de stroom
- A de spanning
- L de weerstand
Later zijn deze letters vervangen door de huidige notatie: I = U R
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345 24
Schrijfwijze
Het hoofdtelwoord geeft de teller van een breuk weer, het rangtelwoord de noemer.
- 1 5 een vijfde, 7 10 zeven tiende, 1 2 6 een twee zesde.
- 11 1 5 elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde.
Enkele breuken hebben een eigen naam:
Een derde lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (derde is het rangtelwoord van drie):
- 1 3 een derde (dus niet eenderde)
- 2 3 twee derde.
sina cosa
- 30-10 5
60 24/60
- Rv = 1 1R1 + R2 +......Rn
1 5
- x(t)
x→(t) = v→ • t + x0→ = dx→ dt • t + x0→
y(p) x(p) = K • G(p) 1 + [K • G(p) • H(p)]
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24
sin a = sin 32 + 18 + 44 60/60 = sin 32,3122
Het eerste voorbeeld is ook als volgt toe te lichten: als men twee taarten elk in vier even grote stukken snijdt, resulteert dat in acht stukken. Ook het delen van breuken is zo te beschrijven: als men anderhalve (1 1⁄2 = 3⁄2) euro uitgeeft aan artikelen die een halve euro per stuk kosten, krijgt men drie van die artikelen, want 3 2 : 1 2 = 3 2 × 2 1 = 3 × 2 2 × 1 = 3.
Groter
|
Op een gegeven moment meent hij, dat hij de zin van het Spel dicht is genaderd, maar denkt toch dat hij dit niet tot zijn beroep moet maken. |
23 • 60 • 60 = 82.800
128 4/ 7 0 achtenveertig achtenveertig
- P = U • I • cos φ
- P = 3U f • I f • cos φ
waarbij:
- U f = U fase en I f = I fase
- P = 3 U fase• I fase • cos φ
- Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon

- Δ BCD ~ Δ ABC
Franciscus 7 feb 2015 12:31 (CET)