Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok: verschil tussen versies
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| Regel 36: | Regel 36: | ||
=Goniometrische verhoudingen= | =Goniometrische verhoudingen= | ||
Goniometrische verhoudingen worden toegepast om bij vraagstukken uit de diverse vakgebieden als de wiskunde, de elektrotechniek en andere disciplines wiskundige berekeningen te kunnen maken. | Goniometrische verhoudingen worden toegepast om bij vraagstukken uit de diverse vakgebieden als de wiskunde, de elektrotechniek en andere disciplines wiskundige berekeningen te kunnen maken. | ||
<br/>In de verhandeling worden deze goniometrische verhoudingen uiteengezet en worden | <br/>In de verhandeling worden deze goniometrische verhoudingen uiteengezet en worden rekenvoorbeelden gegeven. | ||
==Basisbegrippen== | ==Basisbegrippen== | ||
[[Afbeelding:Driehoek ABC.jpg|250px|right]] | [[Afbeelding:Driehoek ABC.jpg|250px|right]] | ||
De afgebeelde rechthoekige driehoek ''ABC'' bevat een aantal goniometrische verhoudingen, die ongeacht de afmetingen van de zijden van de driehoek geldig zijn. Deze goniometrische verhoudingen dienen onder meer om de hoeken van de driehoek te bepalen, maar worden ook in andere disciplines toegepast. | De afgebeelde rechthoekige driehoek '''''ABC''''' bevat een aantal goniometrische verhoudingen, die ongeacht de afmetingen van de zijden van de driehoek geldig zijn. Deze goniometrische verhoudingen dienen onder meer om de hoeken van de driehoek te bepalen, maar worden ook in andere disciplines toegepast. | ||
<br/>De eerste en meest bekende verhouding wordt aangeduid met de '''''sinus''''' van de '''''hoek α''''' meestal afgekort tot '''''sin α'''''. | <br/>De eerste en meest bekende verhouding wordt aangeduid met de '''''sinus''''' van de '''''hoek α''''' meestal afgekort tot '''''sin α'''''. | ||
<br/>De ''sinus'' van een ''hoek α'' wordt als volgt omschreven: | <br/>De ''sinus'' van een ''hoek α'' wordt als volgt omschreven: | ||
| Regel 53: | Regel 53: | ||
==Rekenvoorbeelden== | ==Rekenvoorbeelden== | ||
::'''''Rekenvoorbeeld 1''''' | ::'''''Rekenvoorbeeld 1''''' | ||
::In de eerder afgebeelde driehoek ''ABC'' hebben de zijden de volgende afmetingen: | ::In de eerder afgebeelde driehoek '''''ABC''''' hebben de zijden de volgende afmetingen: | ||
::* '''''AB = 5 cm''''' | ::* '''''AB = 5 cm''''' | ||
::* '''''AC = 4 cm''''' | ::* '''''AC = 4 cm''''' | ||
| Regel 65: | Regel 65: | ||
::'''''Rekenvoorbeeld 2''''' | ::'''''Rekenvoorbeeld 2''''' | ||
[[Afbeelding:Driehoek 30 graden.jpg|280px|right]] | [[Afbeelding:Driehoek 30 graden.jpg|280px|right]] | ||
::De driehoek ''ABC'' in bijgaande afbeelding – als helft van een gelijkzijdige driehoek - heeft de volgende hoeken : | ::De driehoek '''''ABC''''' in bijgaande afbeelding – als helft van een [[Rondom de cirkel|gelijkzijdige driehoek]] - heeft de volgende hoeken : | ||
::* '''''hoek α = 30<sup> 0</sup>''''' | ::* '''''hoek α = 30<sup> 0</sup>''''' | ||
::* '''''hoek γ = 90<sup> 0</sup>''''' | ::* '''''hoek γ = 90<sup> 0</sup>''''' | ||
Versie van 1 sep 2009 13:59
Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)


Franciscus 20 jul 2009 13:33 (UTC)
- sin α = BC / AB = ½ AB / AB = 0,5
- Voor zijde AC wordt de stelling van Pythagoras toegepast, en wel als volgt:
- AC = √ ( AB ) 2 – ( BC ) 2 = √ ( AB ) 2 – ( ½ AB ) 2 = √ ¾ (AB) 2 = ½ AB√3
- Hieruit volgt dan :
- cos α = AC / AB = ½ AB √ 3 / AB = ½ √ 3 ( = 8,66 )
- en :
- tg α = BC / AC = ½ AB / ½ AB√3 = 1/3 . √3 = 0,577
Rondom de cirkel ( 2 )
Goniometrische verhoudingen
Goniometrische verhoudingen worden toegepast om bij vraagstukken uit de diverse vakgebieden als de wiskunde, de elektrotechniek en andere disciplines wiskundige berekeningen te kunnen maken.
In de verhandeling worden deze goniometrische verhoudingen uiteengezet en worden rekenvoorbeelden gegeven.
Basisbegrippen
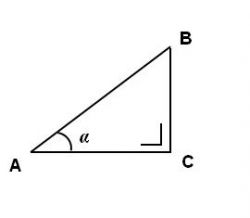
De afgebeelde rechthoekige driehoek ABC bevat een aantal goniometrische verhoudingen, die ongeacht de afmetingen van de zijden van de driehoek geldig zijn. Deze goniometrische verhoudingen dienen onder meer om de hoeken van de driehoek te bepalen, maar worden ook in andere disciplines toegepast.
De eerste en meest bekende verhouding wordt aangeduid met de sinus van de hoek α meestal afgekort tot sin α.
De sinus van een hoek α wordt als volgt omschreven:
- sin α = overliggende rechthoekszijde / schuine zijde = BC / AB.
De tweede goniometrische verhouding – cosinus α ( cos α ) - wordt als volgt omschreven:
- cos α = aanliggende rechthoekszijde / schuine zijde = AC / AB.
Er zijn nog twee goniometrische verhoudingen aan te wijzen, namelijk tangens α ( tan α ) en cotangens α ( cotan α ). Deze twee verhoudingen worden als volgt omschreven:.
- tan α = overliggende rechthoekszijde / aanliggende rechthoekszijde = BC / AC
- en:
- cotan α = aanliggende rechthoekszijde / overliggende rechthoekszijde = AC / BC.
Behalve de vier genoemde verhoudingen, zijn er nog twee goniometrsiche verhoudingen bekend, namelijk secans α ( sec α ) en cosecans α ( cosec α ) .
Aangezien deze twee verhoudingen zelden worden gebruikt, zullen ze in deze verhandeling verder niet worden behandeld
Rekenvoorbeelden
- Rekenvoorbeeld 1
- In de eerder afgebeelde driehoek ABC hebben de zijden de volgende afmetingen:
- AB = 5 cm
- AC = 4 cm
- BC = 3 cm
- Hieruit volgt :
- sin α = BC / AB = 0,6
- cos α = AC / AB = 0,8
- tg α = BC / AC = 0,75
- cotg α = AC / BC = 1,333
- In dit voorbeeld werd nog met getallen gewerkt. In het andere voorbeeld zullen de getallen worden weggelaten, zodat een meer algemener beeld ontstaat. Verder wordt ook de berekening van de cotg niet meer uitgevoerd.
- Rekenvoorbeeld 2
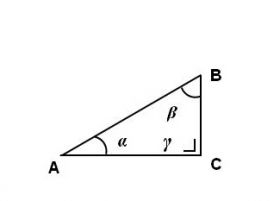
- De driehoek ABC in bijgaande afbeelding – als helft van een gelijkzijdige driehoek - heeft de volgende hoeken :
- hoek α = 30 0
- hoek γ = 90 0
- Aangezien in een driehoek de som van de hoeken 180 0bedraagt, volgt hieruit, dat hoek β = 60 0.
- Aangetoond werd, dat de driehoek de helft is van een gelijkzijdige driehoek, zodat zijde BC = ½ AB.
- De driehoek ABC in bijgaande afbeelding – als helft van een gelijkzijdige driehoek - heeft de volgende hoeken :

