Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok: verschil tussen versies
Geen bewerkingssamenvatting |
|||
| Regel 38: | Regel 38: | ||
<br/>Na een aantal proefnemingen - ook weer door nabootsingen van de praktijkomstandigheden - werd uiteindelijk een eenvoudige oplossing gevonden voor het probleem. | <br/>Na een aantal proefnemingen - ook weer door nabootsingen van de praktijkomstandigheden - werd uiteindelijk een eenvoudige oplossing gevonden voor het probleem. | ||
<br/>Door middel van een aan de bovenzijde van de staven geboorde kamer met een daarin aangebrachte ''remstaaf + olievulling'' - werden de trillingen van de antennestaven tot een ongevaarlijke amplitude teruggebracht. Hierdoor kwam de materiaalspanning '''''σ''''' op de hoogst belaste plaats op ca 30 Nmm<sup>2</sup> uit, dus ver verwijderd van de gevaarlijke spanning die aanvankelijk optrad. | <br/>Door middel van een aan de bovenzijde van de staven geboorde kamer met een daarin aangebrachte ''remstaaf + olievulling'' - werden de trillingen van de antennestaven tot een ongevaarlijke amplitude teruggebracht. Hierdoor kwam de materiaalspanning '''''σ''''' op de hoogst belaste plaats op ca 30 Nmm<sup>2</sup> uit, dus ver verwijderd van de gevaarlijke spanning die aanvankelijk optrad. | ||
<br/>'''''Door deze maatregel zijn in de praktijk ''geen'' breuken meer opgetreden.''''' | <br/>'''''Door deze maatregel zijn in de praktijk ''geen'' breuken van antennestaven meer opgetreden.''''' | ||
==Nawoord== | ==Nawoord== | ||
Versie van 2 feb 2018 17:55
== Deelonderwerp[
http://www.example.com koppelingstekst
'''Voer hier de niet op te maken tekst in''''''''Vetgedrukte tekst''[[[Onderwerp]]]'''] ==
Deelonderwerp ==
Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)
Over vermoeiingsbreuken bij groundplane-antennes

Een veel gebruikte antenne voor voertuigen en schepen is de Groundplane-antenne. Deze heeft als kenmerkende eigenschap, dat geen rekening behoeft te worden gehouden met de richting waarin wordt gezonden of ontvangen, aangezien de antenne een cirkelvormig diagram bezit.
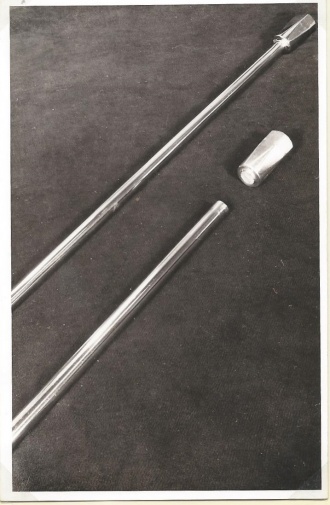
Een bekende opbouw van een groundplane-antenne toont de afbeelding, waarin een straler (a) - bevestigd op een isolator (b) - en een tegencapaciteit (c) staan afgebeeld, gemonteerd op een verzinkt stalen draagmast. Deze draagmast wordt aan boord van schepen met zadels of met beugels aan een reling of een stuurhut bevestigd, vanwaaruit de aansluitkabel naar de zender-ontvanger wordt gevoerd.
De eerder genoemde tegencapaciteit vormt een kunstmatig aardvlak, waardoor de antenne op elke willekeurige hoogte kan worden geplaatst.
Zowel de staven van de straler als van de tegencapaciteit waren bij deze antennes van automatenmessing MS 58 vervaardigd, waarop wegens de optredende klimatologische invloeden een zware nikkellaag (= 25 μm) werd aangebracht.
Breukverschijnselen

Bij een aantal groundplane-antennes van het omschreven type bleken, na enige tijd staven van de tegencapaciteit te zijn afgebroken. Het oppervlak van het breukvlak wees duidelijk in de richting van een vermoeiingsbreuk1), onder meer door de gladde structuur van het vlak en niet-waarneembare vormveranderingen op de breukplaats.
Na uitgebreid onderzoek bleek de breuk van de staven te zijn ontstaan
door gedwongen trillingen die door de scheepsschroef werden opgewekt. De frequentie van deze trillingen ligt bij veel schepen tussen de 20 en 25 hertz (Hz).
Uit verder onderzoek bleek, dat de eigenfrequentie f0 van de antennestaven op 23 Hz lag, waardoor deze gingen meetrillen en resonantie optrad, waardoor zich opslingeringen ontwikkelden die in korte tijd tot breuk moesten leidden. Door deze opslingeringen en de grote amplituden die daardoor ontstonden, werden hoge materiaalspanningen ontwikkeld op de meest gevoelige plek van de staven, namelijk daar waar de staven overgaan in het verbindingsstuk.
Door de hoge materiaalspanningen ontstaan op enkele plekken microscheuren, die elkaar op een geven moment zullen bereiken en daarna samenvallen, waardoor uiteindelijk een breuk wordt gevormd, de vermoeiingsbreuk.
Nader onderzoek
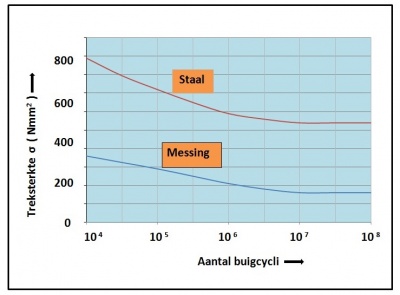
Aangezien de staven door de opslingeringen aan een wisselende belasting werden onderworpen, was het noodzakelijk de gegevens uit de zogenaamde Wöhlerkrommen2) te hanteren. Vastgesteld is namelijk, dat bij wisselende belasting de toegestane materiaalspanning σA van messing asymptotisch meer dan 50% terugloopt, zodat nog maar ca 160 Nmm2 toegestaan is in plaats van 380 Nmm2 die voor statische belastingen geldt.
Uitgaande van een aantal bijkomende factoren als : galvanische bedekking van de staven en de bevestiging ervan in het verbindingsstuk door middel van een stompe las, werd de vermoeiingssterkte δA van het toegepaste MS 58 op de lasplaats nog lager ingeschat, namelijk op 50% van de normale vermoeiingssterkte bij 107 wisselingen, waardoor σA uiteindelijk op ongeveer 80 Nmm2 uitkwam.
Uit verdere proefnemingen, nabootsingen van de praktijkomstandigheden en uit berekeningen bleek de optredende materiaalspanning door de opslingeringen op de breukplaats 100 à 120 Nmm2 te bedragen; dus hogere waarden dan toegestaan.
- Als nagegaan wordt, dat bij de eigenfrequentie f0 van 23 Hz dus 23 x per seconden een volledige amplitude werd doorlopen, dan moest in één uur het aantal wisselingen 23 • 60 • 60 = 82.800 hebben bedragen. Bij continuering zou dan binnen ca 120 uur het aantal wisselingen van 107 zijn bereikt en breuk optreden.
- Deze periode van 120 uur behoeft niet aaneengesloten te zijn geweest, aangezien de schepen in kwestie meestal korte afstanden afleggen.
Toegevoegde demping

Uit het onderzoek was gebleken, dat de demping van messingstaven vrij gering was, waardoor de toegevoegde energie door de trillingen van de scheepsschroef niet werd afgebouwd. Er moest dus een methode worden gevonden om de demping te verhogen.
Na een aantal proefnemingen - ook weer door nabootsingen van de praktijkomstandigheden - werd uiteindelijk een eenvoudige oplossing gevonden voor het probleem.
Door middel van een aan de bovenzijde van de staven geboorde kamer met een daarin aangebrachte remstaaf + olievulling - werden de trillingen van de antennestaven tot een ongevaarlijke amplitude teruggebracht. Hierdoor kwam de materiaalspanning σ op de hoogst belaste plaats op ca 30 Nmm2 uit, dus ver verwijderd van de gevaarlijke spanning die aanvankelijk optrad.
Door deze maatregel zijn in de praktijk geen breuken van antennestaven meer opgetreden.
Nawoord
- Het probleem van de vermoeiingsbreuken, kon worden opgelost door praktijkonderzoek en door theoretische, wiskundige afleidingen. Door dit samenspel werd inzicht verkregen in de aard en de achtergrond van de vermoeiingsproblemen van de messingstaven en kon een oplossing worden gevonden voor het gerezen probleem.
- De genoemde wiskundige afleidingen zijn hier achterwege gelaten, om de leesbaarheid van dit essay niet te verstoren.
Bronvermelding
Bronnen, noten en/of referenties:
- De gegevens van dit essay zijn ontleend aan de verhandeling:
- Tegengaan van vermoeiingsbreuken bij groundplane-antennes door vergroting van de inwendige demping, geschreven door Franciscus.
- 1)De term Vermoeiing geeft door de inzichten die over het verschijnsel bekend zijn, niet de juiste situatie weer. Vermoeiing veronderstelt namelijk ook een periode waarin herstel kan plaatsvinden, en die blijft uit.
- Door het cumulatieve karakter van het proces, gaat na elke willekeurige onderbreking van het proces het vormen van microscheuren onverminderd door. Vanwege het algemene spraakgebruik wordt de term vermoeiing echter gewoon gehandhaafd.
- 2) Zie ook:Metaalmoeheid
De stad Montfort-L'Amaury in eerbetoon aan Maurice Ravel die in dit huis van 1921 tot 1937 woonde
Ravel se fixa à Montfort-l'Amaury en 1921. Sa maison, le Belvédère, conservée en l'état selon la volonté de son frère, abrite un musée depuis 1971 et fait l’objet d’une inscription auprès des monuments historiques depuis 199459.
Français : Maison dite du Belvédère de Maurice Ravel à Montfort-l'Amaury (Yvelines, France)
Date 20 November 2006
Source Cliché personnel, own work
Author ℍenry Salomé (Jaser !) 08:17, 21 November 2006 (UTC)
Object location
48° 46′ 34.28″ N, 1° 48′ 19.4″ E Kartographer map based on OpenStreetMap. View this and other nearby images on: OpenStreetMap - Google Earth info
Licensing[edit]
The copyright holder of this work, hereby publish it under the following licenses:
GNU head Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.
Jabberwocky
NonsenSpoëzie
Onder nonsenspoëzie verstaat men gedichten waarin humoristische fantasie wordt bedreven, en waarin vaak gebruik wordt gemaakt van niet-bestaande woorden en andere dwaasheden.
Het is een subgenre van de poëzie, dat inhoudelijk wordt gekenmerkt door de absurde ideeënwereld die erin wordt opgeroepen, terwijl in de vormgeving vaak een herkenbaar traditioneel metrisch patroon wordt aangehouden. Hierdoor ontstaat veelal een humoristisch effect.
Enkele sprekende voorbeelden van nonsensgedichten zijn:
- Ik ben de blauwbilgorgel
- Op een made
- Hongaarse rapsodie (Rika Csardas)
|
|
Jabberwocky
Eén van de bekendste en aardigste voorbeelden van nonsenspoëzie vinden we in het gedcht Jabberwocky.
Jabberwocky is de oorspronkelijke titel van het beroemde nonsensgedicht van Lewis Carrol, in zijn tweede boek Alice in Spiegelland.
Lewis Carroll was zelf een groot liefhebber van nonsenspoëzie.
Het nonsensgedicht Jabberwocky is een parodie op de oude Duitse ballade: De herder van het Reuzengebergte, waarin een herder een griffioen doodt die zijn schapen aanvalt.
Vertalingen
De bekendste vertaling in het Nederlands is die van Alfred Kossmann uit 1947. In deze vertaling is Jabberwocky : Wauwelwok geworden. In het Frans werd dit:
Jaseroque en in het Duits: Der Jammerwoch.
Wat sterk opvalt in de Nederlandse vertaling, is, dat - hoewel de 'woorden' anders zijn geworden - het ritme van het origineel behouden is gebleven.
- Een vertaling van het origineel maken van traditionele poëzie is al vrij moeilijk,
- aangezien het niet gaat om het letterlijk vertalen maar om de sfeer die in
- het origineel wordt opgeroepen. Toch lukt dit als regel goed, aangezien voor
- ieder woord of uitdrukking in de oorspronkelijke taal wel een corresponderend
- woord of uitdrukking kan worden gevonden. In het gedicht Jabberwocky,
- daarentegen hebben veel woorden geen gewone betekenis, maar is hun enige
- functie het oproepen van een nabijgelegen symbool. Maar wat in de ene taal
- dicht in de buurt ligt, kan in een andere taal vergezocht zijn.
Wauwelwok
In Alice in Spiegelland gaat Alice een ruimte binnen en treft daar een boek aan. Als ze probeert te lezen wat er in staat, gaat het mis, want ze begrijpt niet in welke taal het is geschreven. Ze bladert erin, of ze niet een stuk kon vinden, wat ze kan lezen.
- Want het is allemaal in een taal, die ik niet ken, zei ze tot zich zelf.

Ze piekerde er een poosje over, maar op 't laatst kreeg ze een ingeving.
- Maar natuurlijk, het is een spiegelboek! Als ik het voor een spiegel houd, staan alle woorden weer goed.
'Twas brillig, and the slithy toves
"Beware the Jabberwock, my son!
He took his vorpal sword in hand:
And, as in uffish thought he stood,
One, two! One, two! And through and through
"And hast thou slain the Jabberwock?
'Twas brillig, and the slithy toves
|
't Wier bradig, en de spiramants,
"Pas op de Wauwelwok, mijn kind!
Hij nam zijn gnijpend zwaard ter hand:
En toen hij zat in diep gedenk,
Eén, twee! Hup twee. En door en door
"Hebt gij versnaggeld Wauwelwok?
't Wier bradig en de spiramants,
|
Betekenis

- In het nonsensgedicht Wauwelwok, waarschuwt een vader zijn zoon voor drie
- dieren de Wauwelwok , de Tsjoep-Tsjoep en de Barbeleet die de
- omgeving onveilig maken. Vooral de Wauwelwok is zeer gevaarlijk.
- De jonge zoon gaat er met een zwaard op uit en slaagt erin de
- Wauwelwok te doden. Thuis wordt hij met vreugde ontvangen.
|
|
- Het lijkt erg aardig, zei ze, toen ze het uit had, maar het is erg moeilijk om te begrijpen!
- Ik krijg er wel allerlei ideeën door,
- alleen weet ik niet precies wat ze betekenen! In :ieder geval,
- iemand maakte iets dood dat is alvast duidelijk.
In de origine Engelse uitgave is het 'gedicht' Jabberwocky opgenomen, wat een zogenaamd 'nonsensgedicht' is, ook wel 'nonsenspoëzie' genoemd.
- En nu de Franse en de Duitse versie
Il brilgue: les tôves lubricilleux
"Garde-toi du Jaseroque, mon fils!
Son glaive vorpal en main il va-
Pendant qu'il pense, tout uffusé,
Un deux, un deux, par le milieu,
"As-tu tué le Jaseroque?
Il brilgue: les tôves lubricilleux
|
Es brillig war. Die schlichte Toven
"Bewahre doch vor Jammerwoch!
Er griff sein vorpals Schwertchen zu,
Als stand er tief in Andacht auf,
Eins, Zwei! Eins, Zwei! Und durch und durch
"Und schlugst Du ja den Jammerwoch?
Es brillig war. Die schlichte Toven
|
- OPVS FUNDATUM VATICANVM
- Josephvs Ratzinger - Benedictvs XVI
- - Cooperatores Veritatis -
- OPUS FUNDUM VATICANUM
- Josephus Ratzinger - Benedictus XVI
- - Cooperatores Veritatis -
|
|
span>
- Ook in de bioscoop werden antifascistische acties uitgevoerd
|}
Enkele breuken hebben een eigen naam:
- √12
≈12 1 1 = 1
- 2 0 12 = 1
- 2 1 12 = 1,059463094
- 2 2 12 = 1,122462048
|
|
|
|
|
|
|
|
| Op een gegeven moment stelt hij vast,
dat het een verloren zaak is. |
|---|
|
|
- Het schrijven van de Magister Ludi aan de Pedagogische Dienst
|}
|
|
|
|
{{Overline| (12)}}om ergens een lijntje boven te trekken{{Overline|24}}
12
24
12
--
24
Breuken
a b⁄c: a b/c (geheel getal, teller en noemer) a⁄b: a/b (teller en noemer) 1⁄a: 1/a (alleen noemer)
12
--
24
{{Overline|24}}
12
24
Sjabloon:I =vbreuk
In deze theoretische verhandeling, wordt de vergelijking:
S = A L geïntroduceerd.
Hierbij is:
- S de stroom
- A de spanning
- L de weerstand
Later zijn deze letters vervangen door de huidige notatie: I = U R
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345 24
Schrijfwijze
Het hoofdtelwoord geeft de teller van een breuk weer, het rangtelwoord de noemer.
- 1 5 een vijfde, 7 10 zeven tiende, 1 2 6 een twee zesde.
- 11 1 5 elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde.
Enkele breuken hebben een eigen naam:
Een derde lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (derde is het rangtelwoord van drie):
- 1 3 een derde (dus niet eenderde)
- 2 3 twee derde.
sina cosa
- 30-10 5
60 24/60
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24
sin a = sin 32 + 18 + 44 60/60 = sin 32,3122
Het eerste voorbeeld is ook als volgt toe te lichten: als men twee taarten elk in vier even grote stukken snijdt, resulteert dat in acht stukken. Ook het delen van breuken is zo te beschrijven: als men anderhalve (1 1⁄2 = 3⁄2) euro uitgeeft aan artikelen die een halve euro per stuk kosten, krijgt men drie van die artikelen, want 3 2 : 1 2 = 3 2 × 2 1 = 3 × 2 2 × 1 = 3.
Groter
|
Op een gegeven moment meent hij, dat hij de zin van het Spel dicht is genaderd, maar denkt toch dat hij dit niet tot zijn beroep moet maken. |
23 • 60 • 60 = 82.800
128 4/ 7 0 achtenveertig achtenveertig
- P = U • I • cos φ
- P = 3U f • I f • cos φ
waarbij:
- U f = U fase en I f = I fase
- P = 3 U fase• I fase • cos φ
- Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon
haiku (senryu, tanka, waka) en poëzie (met name haikus) waarin wordt gestreefd op impressionistische wijze de ware essentie te vangen.
Over de eindigheid van driehoeken
Inleiding

- Δ BCD ~ Δ ABC
Franciscus 7 feb 2015 12:31 (CET)

