Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok: verschil tussen versies
Geen bewerkingssamenvatting |
|||
| Regel 113: | Regel 113: | ||
=Logaritmen= | =Logaritmen en exponentiële functies= | ||
==Machtsverheffen== | ==Machtsverheffen== | ||
In [[Rekenkunde ( 3 )]] wordt het onderwerp '''Machtsverheffen''' behandeld. | In [[Rekenkunde ( 3 )]] wordt het onderwerp '''Machtsverheffen''' behandeld. | ||
Versie van 8 dec 2010 14:19
Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)


Beschreibung SAND Maurice Masques et bouffons 07.jpg
Italiano: Scaramuccia Deutsch: Scaramuz Datum 1860(1860)
Quelle SAND Maurice. Masques et bouffons (Comedie Italienne). Paris, Michel Levy Freres, 1860
Urheber Maurice Sand
- 2 2/ 9 + 5/ 9 = 2 7/ 9
Franciscus 20 jul 2009 13:33 (UTC)
- sin α = BC / AB = ½ AB / AB = 0,5
- Voor zijde AC wordt de stelling van Pythagoras toegepast, en wel als volgt:
- AC = √ ( AB ) 2 – ( BC ) 2 = √ ( AB ) 2 – ( ½ AB ) 2 = √ ¾ (AB) 2 = ½ AB√3
- Hieruit volgt dan :
- cos α = AC / AB = ½ AB √ 3 / AB = ½ √ 3 ( = 8,66 )
- en :
- tg α = BC / AC = ½ AB / ½ AB√3 = 1/3 . √3 = 0,577
| Quotiënt | Φ |
|---|---|
| 1 : 1 | 1 |
| 2 : 1 | 2 |
| 3 : 2 | 1,5 |
| 5 : 3 | 1,67 |
| 8 : 5 | 1,6 |
| 13 : 8 | 1.62500 |
| 89 : 55 | 1,6181818 |
| 610 : 377 | 1,61537135 |
| 4181 : 2584 | 1,61803405 |
| 28657 : 17711 | 1,61803399 |
| 196418 : 121393 | 1,618033989 |
Erik Alfred Leslie Satie (Honfleur, 17 mei 1866 – Parijs, 1 juli 1925)

Enkele personages van de Commedia dell'arte zijn:
- Arlecchino
- Brighella
- Capitano
- Colombina
- Dottore
- Isabella
- Pantalone
- Pulcinella
- Scaramouche
Logaritmen en exponentiële functies
Machtsverheffen
In Rekenkunde ( 3 ) wordt het onderwerp Machtsverheffen behandeld.
Hierbij wordt het volgende gesteld:
- Bij het machtsverheffen wordt een getal één, twee of meer keren met zichzelf vermenigvuldigd, waarbij de volgende schrijfwijze wordt gehanteerd:
|
10 1 = 1 • 10 = 10
|
Voorbeeld 1
|
Als het getal 5 een drietal keren met zichzelf wordt vermenigvuldigd, dus:
|
- Als machten moeten worden vermenigvuldigd met andere machten of worden gedeeld door andere machten die hetzelfde grondtal hebben, dan moeten de exponenten van die machten bij elkaar worden opgeteld of worden afgetrokken
|
10 1 • 10 1 kan worden geschreven als : 10 1+1 = 102 = 10 • 10 = 100
|
Exponenten
Het ligt zeer voor de hand te veronderstellen, dat tussen 10 0 en 10 1 of bijvoorbeeld tussen 10 1 en 10 2 ook machten van 10 liggen die een ander getal dan 1, 10 of 100 zouden kunnen opleveren. Dit blijkt inderdaad het geval te zijn.
In Rekenkunde ( 3 ) wordt het onderwerp Worteltrekken behandeld. De ( vierkants )wortel uit bijvoorbeeld 10 wordt aldus genoteerd:
- √ 10 = 3,1622
|
Een andere schrijfwijze voor de wortel uit 10 is 10 1/2 = 10 0,5 wat hetzelfde oplevert, namelijk 3,1622
|
Om elk getal in een exponent uit te kunnen drukken, zijn voor alle getallen tussen 1 en 99 tabellen opgesteld, die deze notering mogelijk maken. Men noemt hierbij het getal 10 het grondtal, hoewel hiervoor ook een ander getal zou kunnen worden gekozen. De exponent van de macht wordt hier mantisse genoemd.
Tabel van mantissen
| Getal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 |
- ∞ |
0000 | 3010 | 4771 | 6021 | 6090 |
7782 |
8451 | 9031 | 9542 | |
| 1 | 0000 | 0414 |
0792 |
1139 | 1461 | 1761 | 2041 | 2304 | 2553 | 2788 | |
| 2 | 3010 | 3222 | 3424 | 3617 | 3802 | 3979 | 4150 | 4314 | 4472 | 4624 | |
| 3 | 4771 | 4914 | 5051 | 5185 | 5315 | 5441 | 5563 | 5682 | 5798 | 5911 | |
| 4 | 6021 | 6128 | 6232 | 6335 | 6435 | 6532 | 6628 | 6721 | 6812 | 6902 | |
| 5 | 6990 | 7076 | 7160 | 7243 | 7324 | 7404 | 7482 | 7559 | 7634 | 7709 | |
| enz → t/m 99 |
Voor getallen < 10 wordt een 0 vóór de mantisse geplaatst. Voor getallen > 10 komt vóór de mantisse een 1 te staan, en bij getallen tussen 100 ( = 10 2 ) en 999 plaatst men een 2 vóór de mantisse. Op die manier is het mogelijk elk denkbaar getal in een exponent vast te leggen.
Voorbeeld 2
|
De mantisse van het getal 6 = 0,7782 → 10
0,7782
= 6
|
Tegenwoordig wordt er niet meer zo uitgebreid gebruik gemaakt van tabellen maar meer van ( wetenschappelijke ) calculators. Ondanks het gemak dat we al lange tijd van deze hulpmiddelen hebben, blijkt het – zeker voor wat de wat ingewikkelde problemen - nog steeds noodzakelijk inzicht te hebben in de basiskennis van de logaritmen, aangezien zonder deze kennis niet wordt begrepen hoe logaritmen werken.
Definitie
Het blijkt dat - met wat hiervoor werd uiteengezet - een definitie is te geven van wat een logaritme van een getal is.
|
Een logaritme van een getal y is de exponent van de macht x waartoe het grondtal moet worden gebracht om het getal y te krijgen. |
Als grondtal wordt – zoals boven werd uitgevoerd - als regel het getal 10 genomen. Hieruit volgt dan:
- y = 10 x
waarbij x de exponent ( mantisse ) is. Deze vorm kan ook op een andere manier worden geschreven, namelijk:
- x = 10 log y
waarbij log de afkorting van de logaritme van het getal y voortelt.
Voorbeeld 3
|
De logaritme van het getal 8, is te schrijven als: 8 = 10 x , en x = 10 log 8
|
Voor de goede orde zou eigenlijk vóór de logaritme steeds de exponent 10 moeten worden genoteerd,
dus 10 log a. In de praktijk laat men voor het gemak meestal de aanduiding 10 vóór de logaritme weg.
Formules
Algemeen gelden de volgende formules:
- log a • b = log a + log b
- log a : b = log a - log b
- log an = n log a
- log n√ a = 1/n log a
Voorbeeld 3
|
In de vorm: log a • b = log a + log b, wordt voor a en b ingevuld: log 3 • 4 = log 3 + log 4
|
Voorbeeld 4
|
In de vorm: log a : b = log a - log b, wordt voor a en b ingevuld: log 8 : 4 = log 8 - log 4
|
Voorbeeld 5
|
In de vorm: log n√ a = 1/n log a wordt voor a en n ingevuld: log √ 9 = 1/2 log 9 *)
|
*) Voor n√ a wordt bij een 2emachtswortel meestal gewoon √ a geschreven, dus met weglating van de 2 boven het wortelteken.
Voorbeeld 6
|
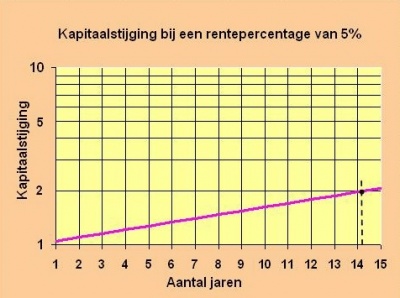
Nagegaan wordt hoeveel jaar een kapitaal X, uitgezet tegen 5%, zal zijn verdubbeld
|
In onderstaande grafiek wordt nog duidelijker hoe deze kapitaalstijging in de tijd verloopt. De y-as van de grafiek heeft een logaritmische schaal, waardoor de stijgende lijn van de grafiek een rechte lijn wordt. Goed te zien is, dat na ca 14 jaar het uitgezette kapitaal is verdubbeld.
Briggse en natuurlijke logaritmen
De tot nu toe gehanteerde logaritmen - met als grondtal 10 - worden ook wel Briggse logaritmen genoemd, naar de wiskundige Henry Briggs. Naast deze logaritmen bestaat ook de natuurlijke of Neperse logaritme met als grondtal e, naar de wiskundige John Napier ( Neper ), waarbij e = 2,7182818.......
De notatie voor de Briggse logaritmen is - zoals al uiteengezet - als volgt:
- 10 log x = log x
De notatie voor de natuurlijke logaritme is als volgt:
- e log x = ln x
Om Briggse logaritmen naar de natuurlijke logaritmen te kunnen omrekenen, geldt:
- log x = 0,4343... ln x
en omgekeerd:
- ln x = 2,3026.... log x
Exponentiële functies
Met Voorbeeld 6 over de kapitaalvermeerdering is gelijk een overstap gemaakt naar de exponentiéle functies.
John Napier (Neper) stelde in 1614 de eerste logaritmen voor met e (2,71828...) als keuze voor het grondtal. Daarmee kon men ingewikkelde berekeningen in de sterrenkunde reeds vereenvoudigen. Toch waren de berekeningen met het grondtal e nog vaak erg moeilijk, waardoor Briggs voorstelde grondtal 10 toe te passen.
uitvinder • gebruikt
